جواب فعالیت صفحه 6 ریاضی نهم
1- جدول عددهای صحیحِ زیر را طوری کامل کنید که مجموع عددهای روی هر سطر، هر ستون و هر قطرِ آن برابر ١٢ شود؛ سپس مجموعهٔ عددهای سطر دوم جدول را بنویسید و آن را A بنامید.
$A=\left\{ 6,4,2 \right\}$
| 12 | 10- | 10 |
| 2 | 4 | 6 |
| 2- | 18 | 4- |
اکنون مجموعه B را چنان بنویسید که شامل سه عدد زوج متوالی و میانگین عضوهای آن با 4 برابر باشد. هریک از مجموعههای A و B چند عضو دارد؟
$B=\left\{ 2,4,6 \right\}$
آیا هر عضو A در مجموعهٔ B است؟
بلهآیا هر عضو B در مجموعهٔ A است؟
بله2- مجموعهٔ A شامل سه عدد طبیعی متوالی است به طوری که حاصل جمع آنها برابر 27 است. ابتدا A را با عضوهای آن بنویسید؛ سپس مجموعههایی را مشخص کنید که در زیر معرفی شده و با A برابر است:
$A=\left\{ 8,9,10 \right\}$الف) مجموعهٔ عددهای طبیعی بین 6 و 10: $A=\left\{ 7,8,9 \right\}$
ب) مجموعهٔ عددهای طبیعی بزرگتر از ٧ و کوچکتر از 11: $B=\left\{ 8,9,10 \right\}$
ج) مجموعهٔ سه عدد طبیعی متوالی که میانگین آنها با 9 برابر است: $C=\left\{ 8,9,10 \right\}$
جواب کار در کلاس صفحه 6 ریاضی نهم
1- جاهای خالی را در مجموعههای زیر طوری پرکنید که مجموعهها برابر باشد:
الف) $\left\{ 5,3,\frac{2}{5},4,\frac {9}{3} \right\}=\left\{ \frac{5}{2},3,\frac{-\sqrt{144}} {{{\left( -2 \right)}^{2}}},4,\sqrt{25} \right\}$
ب) $\left\{ 7,\frac{4}{10},\sqrt{\frac {4}{9},}-\frac{1}{2},-2,0/625 \right\}=\left\{ \frac{2} {3},\frac{2}{5},-0/5,\frac{5}{8},7,-2 \right\}$
2- دو مجموعه به نام های A و B مانند سؤال بالا طرح کنید. پاسخ خود را با دوستانتان مقایسه کنید.
$A=\left\{ 1,23,-1,\frac{3}{5} \right \}$
$B=\left\{ {{1}^{4}},\sqrt[3]{27},- \sqrt{\frac{9}{25}},\sqrt[3]{-1},(\frac{8}{4}) \right \}$
جواب فعالیت صفحه 7 ریاضی نهم
مجموعهٔ عددهای جدول فعالیت قبل را D بنامید؛ سپس عضوهای مجموعه D را در نمودار وِن روبهرو بنویسید:
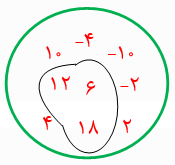
$D=\left\{ 10,-10,12,6,4,2,-4,18,-2 \right\}$
در نمودار بالا، عضوهایی را که بر 3 بخش پذیر است با یک منحنی بسته مشخص کنید و B بنامید.
$B=\left\{ 6,12,18 \right\}$
مجموعه B را بنویسید. آیا هر عضو B، عضوی از D نیز هست؟
بلهدر مجموعه D، عددهای زوج را مشخص کنید و آن را C بنامید؛ آیا $D=C$ ؟خیر
$C=\left\{ 10,6,2,12,18 \right\}$
آیا مجموعه C زیر مجموعه D است؟ خیر
اکنون زیرمجموعهای از D را مشخص کنید که عضوهای آن عددهای فرد باشد؛ نام دیگر این مجموعه چیست؟
$\left\{ {} \right\}$ نام دیگرش (تهی) میباشد.
آیا عبارت $\left\{ 10,4,-6,2 \right \}\subseteq D$ درست است؟ چرا؟
خیر، زیرا $-6\notin D$
آیا در مجموعهٔ تُهی عضوی هست که در مجموعهٔ دلخواهی مانند A نباشد؟
خیرجواب کار در کلاس صفحه 8 ریاضی نهم
1- با توجه به نمودار زیر، دلیل درستی یا نادرستی عبارتهای زیر را مشخص کنید:
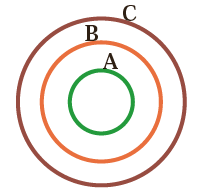
| عبارت | وضعیت | دلیل |
| $A\nsubseteq C$ | نادرست | همهٔ عنصرهای A در C هستند. |
| $B\subseteq A$ | نادرست | عنصرهایی از B در A نیستند.($B \gt A $) |
| $C\nsubseteq A$ | نادرست | عنصرهایی از C در A نیستند. |
| $\varnothing \subseteq A$ | درست | تهی زیر مجموعه هر مجموعهای است. |
| $B\subseteq C$ | درست | همهٔ اعضای B در C هستند. |
| $A\subseteq B$ | درست | همهٔ اعضای A در B هستند. |
2- مجموعههای A، B و C را در نظر بگیرید؛ سپس درستی یا نادرستی عبارت های زیر را مشخص کنید (با ذکر دلیل):
$A=\left\{ 1,3,6,4 \right\}$
$B=\left\{ 5,1,3 \right\}$
$C=\left\{ 2,5,1,3,6 \right\}$
| عبارت | وضعیت | دلیل |
|---|---|---|
| $B\nsubseteq A$ | درست | $5\notin A$ |
| $3\subseteq B$ | نادرست | $3\in B$ |
| $A\subseteq B$ | نادرست | $6,4\notin B$ |
| $B\subseteq C$ | نادرست | همه اعضای B در C هستند. |
| $A\nsubseteq C$ | نادرست | $4\notin C$ |
| $2\in A$ | نادرست | عدد 2 بین $A=\left\{ 1,3,6,4 \right\}$ نیست. |
| $\left\{ 1.4 \right\}\in A$ | نادرست | |
| $6\notin A$ | نادرست | عدد 6 بین $A=\left\{ 1,3,6,4 \right\}$ هست. |
| $\left\{ 5,6 \right\}\subseteq C$ | درست | |
| $5\in C$ | درست | عدد 5 بین $C=\left\{ 2,5,1,3,6 \right\}$ هست. |
| $0\subseteq A$ | نادرست | عدد 0 در $A=\left\{ 1,3,6,4 \right\}$ قرار ندارد. |
3- همهٔ زیرمجموعههای $A=\left\{ a,b,c \right\}$ در زیر نوشته شده است:
$\varnothing ,\left\{ a \right\},\left\{ b \right\},\left\{ c \right\},\left\{ a,b \right\},\left\{ a,c \right\},\left\{ b,c \right\},\left\{ a,b,c \right\}$
مانند نمونه، تمام زیرمجموعههای هریک از مجموعههای زیر را بنویسید:
الف) مجموعهٔ عددهای طبیعی بین 9 و 12.
$\left\{ 10 \right\},\left\{ 11 \right \},\left\{ 12 \right\},\left\{ 10,11 \right\},\left\{ 10,12 \right\},\left\{ 11,12 \right\}\left\{ 10,11,12 \right\}$
ب) $\left\{ a,b,c,d \right\}$
$\varnothing ,\left\{ a \right\},\left\{ b \right\},\left\{ c \right\},\left\{ d \right\},\left\{ a,b \right\},\left\{ a,c \right\},\left\{ a,d \right\}, \left\{ b,c \right\},\left\{ b,d \right\},\left\{ c,d \right\},\left\{ a,b,c \right\},\left\{ a,b,d \right\}, \left\{ b,c,d \right\},\left\{ c,d,a \right\},\left\{ a,b,c,d \right\}$
جواب کار درکلاس صفحه 10 ریاضی نهم
مجموعههای زیر را با عضوها مشخص کنید:
الف) مجموعهٔ عددهای صحیح فرد:
$\left\{ ...,-3,-1,1,3,5,7,... \right \}$
ب) $A=\left\{ \left. x \right|x\in \mathbb{Z},-5\le x\le 5 \right\}$
$\left\{ -5,-4,-3,-2,...,1,2,3,4 \right\}$
ج) $B=\left\{ \left. 3k+2 \right|k\in \mathbb{Z} \right\}$
$\left\{ ....,-4,-1,2,5,8,10,... \right\}$
جواب تمرین صفحه 10 ریاضی نهم
1- مجموعهٔ $A=\left\{ -2,-1,0,1,2 \right \}$ را در نظر بگیرید. کدام یک از مجموعههای زیر با هم برابر است؟
B و C$B=\left\{ \left. x \right|x\in A,{{x} ^{2}}\le 2 \right\}$
$B=\left\{ -1,0,1 \right\}$
$C=\left\{ \left. x \right|x\in A,-1\le x\le 1 \right\}$
$C=\left\{ -1,0,1 \right\}$
$D=\left\{ \left. x \right|x\in A,{{x} ^{4}}=1 \right\}$
$D=\left\{ -1,1 \right\}$
2- سه مجموعه مانند A و B و C بنویسید به طوری که $A \subseteq B$ و $B\subseteq C$ آیا میتوان نتیجه گرفت $A\subseteq C$ ؟
بله$A=\left\{ 1 \right\}$
$B=\left\{ 1,2 \right\}$
$C=\left\{ 1,2,3 \right\}$
3- تمام زیرمجموعههای هریک از مجموعههای زیر را بنویسید:
الف) $A=\left\{ \left. x \right|x\in \mathbb{N},2x+1=3 \right\}$
$A=\left\{ 1 \right\}\to \varnothing , \left\{ 1 \right\}$
$B=\left\{ \left. 2x \right|x=0,2,3 \right\}$
$B=\left\{ 0,4,6 \right\}\to \varnothing ,\left\{ 0 \right\},\left\{ 4 \right\},\left\{ 6 \right\},\left\{ 0,4 \right\},\left\{ 0,6 \right\}, \left\{ 4,6 \right\},\left\{ 0,4,6 \right\}$
4- نمودار زیر، وضعیت مجموعههای $\mathbb{Q}$، $ \mathbb{W}$، $\mathbb{N}$، $\mathbb{Z}$ را نسبت به هم نشان میدهد؛ آنها را نام گذاری و با علامت $\subseteq$ باهم مقایسه کنید.
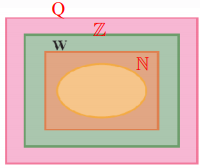
$\mathbb{N}\subseteq \mathbb{W} \subseteq \mathbb{Z}\subseteq \mathbb{Q}$
5- درستی یا نادرستی عبارتهای زیر را با ذکر دلیل مشخص کنید:
| عبارت | وضعیت | دلیل |
|---|---|---|
| الف) هر عدد گویا عددی حسابی است. | نادرست | $\frac{1}{3}\in \mathbb{Q}$ |
| ب) هر عدد حسابی عددی گویا است. | درست | $\mathbb{W} \subseteq \mathbb{Q}$ |
| ج) هر عدد صحیح عددی گویا است. | درست | $\frac{1}{3}\notin \mathbb{W}$ |
| د) بعضی از عددهای گویا، عدد صحیح است | درست | $\mathbb{Z}\subseteq \mathbb{Q}$ |


