جواب فعالیت صفحه ۸ ریاضی (۱) دهم
الف) دو مجموعهٔ زیر را در نظر بگیرید و اعضای هر یک را روی محور نشان دهید.
\begin{align} & A=\{x\in \mathbb{Z}|-۳ \lt x \le ۲\} \\ \end{align}

\begin{align} & B=\{x\in \mathbb{R}|-۳ \lt x \le ۲\} \\ \end{align}

ب) $A$ را با نمایش اعضا و $B$ را به صورت یک بازه بنویسید.
$A=\left\{ -۲,-۱,۰,۱,۲ \right\} \\ B=(-۳,۲]$
پ) در مورد $A$، اگر مجموعهٔ مرجع را $\mathbb{Z}$ در نظر بگیریم، $A'$ را مشخص کنید.
$A'=\mathbb{Z}-A=\left\{ ...,-۴,-۳,۳,۴,۵,... \right\}$
ت) در مورد $B$ با فرض این که $\mathbb{R}$ مجموعهٔ مرجع باشد، $B'$ را مشخص کنید و آن را روی محور نمایش دهید.
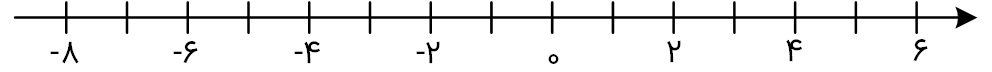
$$B'=\mathbb{R}-(-۳,۲]=(-\infty ,-۳]\bigcup (۲,+\infty )$$

جواب کار در کلاس صفحه ۸ ریاضی (۱) دهم
۱- اگر $U$ مجموعهٔ شامل تمام استانهای کشورمان باشد و $A$ مجموعهٔ استانهای غیرساحلی، آنگاه $A'$ را با نمایش اعضای آن بنویسید.
$A'=${گلستان، مازندران، گیلان، سیستان و بلوچستان، هرمزگان، بوشهر، خوزستان}
۲- فرض کنیم $U$ مجموعهٔ تمام اتومبیلهای پلاک گذاری شدهٔ کشور و $B$ مجموعهٔ اتومبیلهای با پلاک فرد باشد. در این صورت $B'$ چه مجموعهای خواهد بود؟
$B'$ مجموعهٔ اتومبیلهای با پلاک زوج میباشد.
۳- با فرض آنکه $\mathbb{N}$ مجموعه مرجع باشد، هر مجموعه را به متمم خودش وصل کنید.
$\{۱,۳,۵,۷,۹,...\} \Rightarrow \{۲,۴,۶,۸,۱۰,...\} \\ \{۳,۶,۹,۱۲,...\} \Rightarrow \{۱,۲,۴,۵,۷,۸,...\} \\ \{۱,۲,۳,...,۹\} \Rightarrow \{۱۰,۱۱,۱۲,۱۳,۱۴,...\} \\ \{۲,۳,۵,۷,۱۱,۱۳,...\} \Rightarrow \{۱,۴,۶,۸,۹,۱۰,۱۲,۱۴,...\}$
۴- $U$ مجموعهٔ مرجع و $A$ زیرمجموعهٔ دلخواهی از آن میباشد. طرف دوم تساویهای زیر را بنویسید.
$ A\bigcap A'=\varnothing \\ A\bigcup A'=U \\ U'=\varnothing \\ \varnothing '=U $
۵- الف) اگر $\mathbb{Z}$ را به عنوان مجموعهٔ مرجع در نظر بگیریم، آنگاه $\mathbb{N}'$ را با نوشتن اعضای آن مشخص کنید.
اگر $Z$ مجموعهٔ مرجع باشد:
\begin{align} & N'=\left\{ ...,-۳,-۲,-۱,۰ \right\} \\ \end{align}
ب) اگر $\mathbb{Z}$ را به عنوان مجموعهٔ مرجع در نظر بگیریم، در این صورت $\mathbb{N}'$ روی محور نمایش دهید.
اگر $R$ مجموعهٔ مرجع باشد:

۶- فرض کنیم $U=\{۱,۲,۳,۴,۵\}$ مجموعه مرجع باشد و $A=\{۱,۲,۳\}$ و $B=\{۲,۴\}$. ابتدا $A'$ و $B'$ را بنویسید و سپس جدولهای زیر را کامل کنید. از هر قسمت چه نتیجهای میگیرید؟
${A}'=\{۴,۵\} {B}'=\{۲,۴\}$
| $A'\bigcap B'$ | $(A\bigcup B)'$ | $A\bigcup B$ |
| $\{۵\}$ | $\{۵\}$ | $\{۱,۲,۳,۴\}$ |
نتیجه:
$(A\bigcup B)'=A'\bigcap B'$
| $A'\bigcup B'$ | $(A\bigcap B)'$ | $A\bigcap B$ |
| $\{۱,۳,۴,۵\}$ | $\{۱,۳,۴,۵\}$ | $\{۲\}$ |
نتیجه:
$(A\bigcap B)'=A'\bigcup B'$
| $A\bigcap B'$ | $A-(A\bigcap B)$ | $A-B$ |
| $\{۱,۳\}$ | $\{۱,۳\}$ | $\{۱,۳\}$ |
نتیجه:
$A-B=A-(A\bigcap B)=A\bigcap B'$
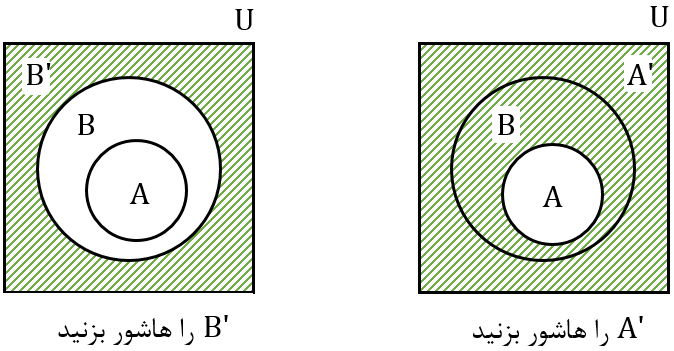
الف) فرض کنیم $A\subseteq B\subseteq U$ که در آن $U$ مجموعهٔ مرجع است. در نمودارهای مقابل $A'$ و $B'$ را مشخص کنید و سپس تعیین کنید که آیا بین $A'$ و $B'$ هم رابطهٔ زیر مجموعه بودن برقرار است؟ چگونه؟
بله، با توجه به نمودار ون مشخص میشود که $B'$ زیرمجموعه $A'$ است. ($B'\subseteq A'$)
ب) اگر $U=\{a,b,c,d,e\}$ مجموعهٔ مرجع باشد و $A=\{a,b\}$ و $B=\{a,b,c\}$، در این صورت $A\subseteq B$ میباشد. با به دست آوردن $A'$ و $B'$ نشان دهید که بین $A'$ و $B'$ هم رابطه زیر مجموعه بودن برقرار است.
\begin{align} & \left. \begin{matrix} A'=\{c,d,e\}\begin{matrix} \\ \end{matrix}\text{ }\!\!~\!\!\text{ } \\ \text{ }\!\!~\!\!\text{ }\!\!~\!\!\text{ }B'=\{d,e\} \\ {} \\ \end{matrix} \right\}\Rightarrow B'\subseteq A' \\ \end{align}
جواب فعالیت صفحه ۱۰ ریاضی (۱) دهم
۱- یک تیم کوه نوردی متشکل از ۴ دانش آموز و ۳ دانشجوی عضو یک مؤسسهٔ طرفدار محیط زیست است. اعضای این تیم به طور داوطلبانه در روزهای جمعهٔ هر هفته کوههای اطراف شهر خود را از وجود زباله پاک سازی میکنند.
اعضای دانش آموز این تیم مجموعه {آنیتا، زهرا، الناز، الهام}=A و اعضای دانشجوی آن مجموعه {فاطمه، معصومه، فرزانه}=B هستند. همان گونه که دیده میشود، این دو مجموعه هیچ عضو مشترکی ندارند؛ به عبارت دیگر $A\bigcap B=\varnothing $
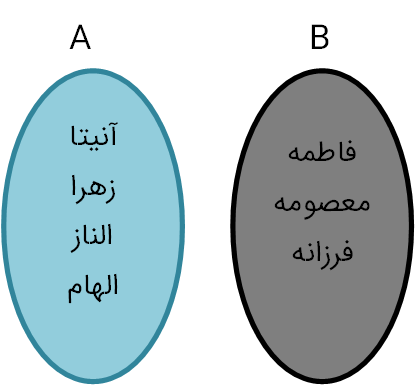
الف) اعضای $A\bigcup B$ را که بیانگر اعضای تیم کوه نوردی میباشد، بنویسید و جدول زیر را تکمیل کنید.
{فاطمه، معصومه، فرزانه، آنیتا، زهرا، الناز، الهام}
| $n(A\bigcap B)$ | $n(A\bigcup B)$ | $n(B)$ | $n(A)$ |
| ۰ | ۷ | ۳ | ۴ |
ب) تعداد عضوهای $A\bigcup{B}$ چه رابطهای با $n(A)$ و $n(B)$ دارد؟ این رابطه را به صورت یک فرمول بنویسید.
$A\bigcap B=\varnothing \Rightarrow n(A\bigcup B)=n(A)+n(B) \\ n(A\bigcup B)=۴+۳=۷$
تعداد عضوهای $A\bigcup{B}$ از مجموع عضوهای A و B تشکیل شده است.
پ) تحت چه شرایطی این فرمول برای دو مجموعه دلخواه $A$ و $B$ برقرار است؟
این فرمول هنگامی برقرار است که اشتراک دو مجموعهٔ $A$ و $B$ هیچ عضوی نداشته باشد.
۲ الف) مجموعهٔ شمارندههای طبیعی دو عدد ۲۸ و ۳۰ را به ترتیب $A$ و $B$ مینامیم. موارد خواسته شده را بنویسید.
مجموعه شمارندههای عدد ۲۸:
$A=\{۱,۲,۴,۷,۱۴,۲۸\} \\ n(A)=۶$
مجموعه شمارندههای عدد ۳۰:
$B=\{۱,۲,۳,۵,۶,۱۰,۱۵,۳۰\} \\ n(B)=۸$
شمارندههای مشترک ۲۸ و ۳۰:
$A\bigcap B=\{۱,۲\} \\ n(A\bigcap B)=۲ \\ \\ \\ A\bigcup{B}=\{۱,۲,۳,۴,۵,۶,۷,۱۰,۱۴,۱۵,۲۸,۳۰\} \\ n(A\bigcup{B})=۱۲$
ب) جدول زیر را کامل کنید.
| $n(A\bigcup B)$ | $n(A\bigcap B)$ | $n(B)$ | $n(A)$ |
| ۱۲ | ۲ | ۸ | ۶ |
پ) چرا رابطهای را که در فعالیت (۱) به دست آوردید؛ یعنی $n(A\bigcup B)=n(A)+n(B)$ در این مثال برقرار نیست؟
برای اینکه در فعالیت (۱) دو مجموعهٔ $A$ و $B$ هیچ اشتراکی نداشتند. اما در این مثال اشتراک دو مجموعه $A$ و $B$ دارای دو عضو میباشند.
ت) با تکمیل نمودار مقابل، سعی کنید رابطهٔ درست برای $n(A\bigcup B)$ را حدس بزنید.
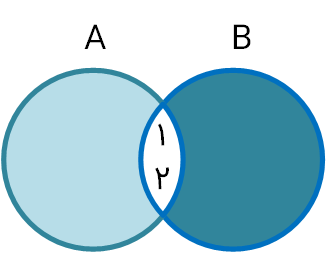
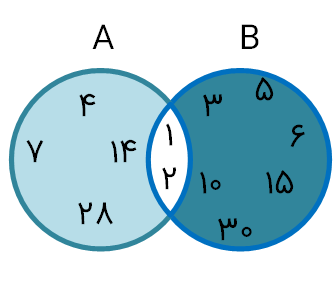
$n(A\bigcup B)=n(A)+n(B)-n(A\bigcap B)$
جواب فعالیت صفحه ۱۱ ریاضی (۱) دهم
۱- یک دوره جشنوارهٔ فیلم کوتاه با شرکت ۲۱ فیلم در موضوعات مختلف در حال برگزاری است که در بین آنها ۷ فیلم پویانمایی (کارتونی) و ۸ فیلم طنز وجود دارد، به طوری که ۳ تا از فیلمهای پویانمایی با مضمون طنز میباشند. مطلوب است تعداد کل فیلمهایی که:
الف) پویانمایی یا طنزند.
ب) غیرپویانمایی و غیر طنزند.
روش اول حل: مجموعهٔ شامل تمام فیلمها را با $U$، مجموعه فیلمهای پویانمایی را با $C$ و مجموعه فیلمهای طنز را $T$ نشان میدهیم. جاهای خالی را پر کنید و جوابها را بیابید.
$n(C\bigcup T)=n(C)+n(T)-n(C\bigcap T) \\ ۷+۸-۳=۱۲۵$
$n(C\bigcup{T})'=n(U)-n(C\bigcup T) \\ ۲۱-۱۲=۹$
روش دوم حل: در نمودار وِن مقابل، دو مجموعهٔ $C$ و $T$ سطح درون $U$ را به چهار ناحیهٔ جداگانه تقسیم کردهاند که عدِد مربوط به دوتا از نواحی نوشته شده است. با نوشتن اعداد مربوط به دو قسمت دیگر، جواب قسمتهای (الف) و (ب) را بیابید.
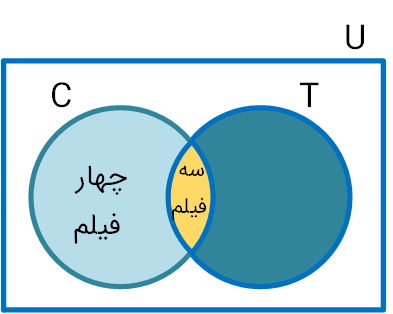
الف:
$n(C\bigcup{T})=۴+۳+۵=۱۲$
ب:
$n(C\bigcup{T})'=۲۱-۱۲=۹$
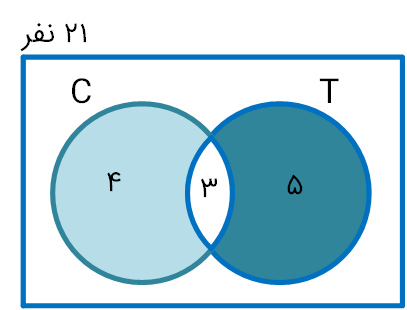
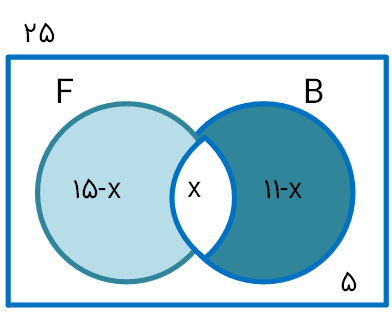
۲- در یک کلاس ۲۵ نفری، تعداد ۱۵ نفر عضو تیم فوتبال و ۱۱ نفر عضو تیم بسکتبال کلاس هستند. اگر ۵ نفر از دانش آموزان این کلاس عضو هیچ یک از این دو تیم نباشند، مشخص کنید چند نفر از آنها عضو هر دو تیم هستند.
روش اول حل: با تکمیل نمودار زیر مقدار $X$ را بیابید.
$۱۵-x+x+۱۱-x=۲۵-۵ \\ \Rightarrow x=۶$
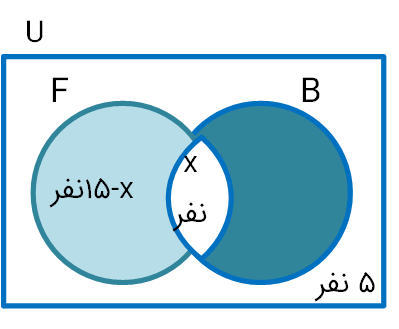
روش دوم حل: چون ۵ نفر عضو هیچ یک از این دو تیم نیستند، پس $n(B\bigcup F)=۲۰$. حال با نوشتن فرمول $n(B\bigcup F)$ میتوان $n(B\bigcap F)$ را به دست آورید.
اگر $n(A)$ تعداد دانش آموزانی باشند که در تیم فوتبال و $n(A)$ تعداد دانش آموزانی باشند که در تیم بسکتبال عضو میباشند در این صورت داریم:
$n(A\bigcup B)=۲۵-۵=۲۰$
تعداد دانش آموزانی باشند که عضو فوتبال یا بسکتبال میباشند.(۲۰ نفر)
$n(A\bigcup B)=n(A)+n(B)-n(A\bigcap B) \\ ۲۰=۱۵+۱۱-n(A\bigcap B) \\ \Rightarrow n(A\bigcap B)=۲۶-۲۰=۶$
تعداد دانش آموزانی که در هر دو تیم عضو میباشند.(۶ نفر)
جواب تمرین صفحه ۱۲ ریاضی (۱) دهم
۱- $\mathbb{R}$ را به عنوان مجموعهٔ مرجع در نظر بگیرید و سپس متمم هر یک از مجموعههای زیر را روی محور نشان دهید.
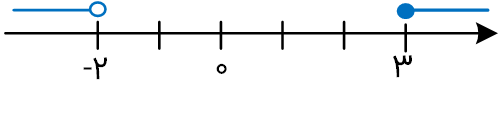
$A=[-۲,۳]$
$A'=(-\infty ,-۲)\bigcup [۳,+\infty ]$
$B=\{۰,۱,۲,۳,۴,...\}$
$B'=R-W$

$C=(۰,+\infty )$
$C'=(-\infty ,۰]$

$D=(-\infty ,۱)$
$D'=(۱,+\infty )$

۲- $\mathbb{N}$ را به عنوان مجموعه مرجع در نظر بگیرید.
الف) مجموعهای نامتناهی مثل $A$ مثال بزنید که $A'$ هم نامتناهی باشد.
$A=\left\{ ۳,۶,۹,... \right\} \\ A'=\left\{ ۱,۲,۴,۵,... \right\}$
ب) مجموعهای نامتناهی مثل $B$ مثال بزنید که $B'$ هم متناهی باشد.
$B=\left\{ ۲,۳,۴,... \right\} \\ B'=\left\{ ۱ \right\}$
پ) مجموعهای متناهی $C$ مثال بزنید و $C'$ را به دست آورید. $C'$ متناهی است یا نامتناهی؟
$C=\left\{ ۱,۲,۳\right\} \\ C'=\left\{ ۴,۵,۶,... \right\}$
$C'$ نامتناهی میباشد.
۳- اگر $n(A)=۱۵$، $n(A\bigcap B)=۵$ و $n(A\bigcup B)=۳۰$ آنگاه $n(B)$ را محاسبه کنید.
$n(A)=۱۵ \\ n(A\bigcap B)=۵ \\ n(A\bigcup B)=۳۰ \\ n(A\bigcup B)=n(A)+n(B)-n(A\bigcap B) \\ ۳۰=۱۵+n(B)-۵ \\ n(B)=۳۰-۱۰=۲۰$
۴- فرض کنیم $A$ و $B$ زیر مجموعههایی از مجموعهٔ مرجع $U$ باشند، به طوری که $n(U)=۱۰۰$، $n(A)=۶۰$، $n(B)=۴۰$ و $n(A\bigcap B)=۲۰$ مطلوب است:
الف: $n(A\bigcup B)$
$n(A\bigcup B)=n(A)+n(B)-n(A\bigcap B) \\ =۶۰+۴۰-۲۰=۸۰$
ب: $n(A\bigcap B')$
$n(A\bigcap B')=n(A-B)=n(A)-n(A\bigcap B) \\ ۸۰-۴۰=۴۰$
پ: $n(A'\bigcap B)$
$n(A'\bigcap B)=n(B-A)=n(B)-n(B\bigcap A) \\ ۸۰-۶۰=۲۰$
ت: $n(A'\bigcap B')$
$n(A'\bigcap B')=n[(A\bigcup B)'] \\ n(U)-n(A\bigcup B) \\ ۱۰۰-۸۰=۲۰$
۵- در یک کلاس ۳۱ نفری، تعداد ۱۴ نفر از دانش آموزان عضو گروه سرود و ۱۹ نفر آنها عضو گروه تئاترند. اگر ۵ نفر از دانش آموزان این کلاس عضو هر دو گروه باشند، مطلوب است:
تعداد کل دانش آموزان کلاس: $n(U)=۳۱$
تعداد دانش آموزان گروه سرود: $n(A)=۱۴$
تعداد دانش آموزان گروه تئاتر: $n(B)=۱۹$
تعداد دانش آموزان عضو هر دو گروه: $n(A\bigcap B)=۵$
الف) تعداد دانش آموزانی که فقط عضو گروه سرودند.
$n(A)-n(A\bigcap B) \\ ۱۴-۵=۹$
ب) تعداد دانش آموزانی که عضو هیچ یک از این دو گروه نیستند.
$n(U)-n(A\bigcup B) \\ ۳۱-۲۸=۳$
۶- در یک نظرسنجی از ۱۱۰ مشتری یک فروشگاه زنجیرهای، مشخص شد که ۷۰ نفر آنها در یک ماه گذشته از محصولات شرکت $A$ و ۵۷ نفرشان از محصولات شرکت $B$ خرید کردهاند. همچنین ۳۲ نفر از آنان نیز اعلام کردند که در این مدت از هر دو شرکت خرید کردهاند. چه تعداد از این ۱۱۰ نفر در یک ماه گذشته:
:تعداد کل مشتری:
$n(U)=۱۱۰$
تعداد افرادی که از محصول $A$ خریداری کردهاند:
$n(A)=۷۰$
تعداد افرادی که از محصول $B$ خریداری کردهاند:
$n(B)=۵۷$
تعداد افرادی که از هر دو شرکت خرید داشتهاند:
$n(A\bigcap B)=۳۲$
الف) دست کم از یکی از این دو شرکت خرید کردهاند.
$n(A\bigcup B)=n(A)+n(B)-n(A\bigcap B) \\ ۷۰+۵۷=۹۵$
ب) فقط از شرکت $A$ خرید کردهاند.
$n(A-B)=n(A)-n(A\bigcap B) \\ ۷۰-۳۲=۳۸$
پ) دقیقاً از یکی از این دو شرکت خرید کردهاند.
$$n(B-A)=n(B)-n(A\bigcap B) \\ ۵۷-۳۲=۲۵$$
۲۵ نفر فقط از شرکت $B$ خرید کردهاند.
۳۸ نفر هم فقط از شرکت $A$ خرید کرده اند.
$$۳۸+۲۵=۶۳$$
بنابراین ۶۳ نفر دقیقاً از یکی از این دو شرکت خرید داشتهاند.
نکته: تعداد عضوهایی که فقط در $A$ یا فقط در $B$ میباشند برابر است با:
$$n(A\bigcup B)-n(A\bigcap B)$$
به عبارت دیگر تعداد عضوهای این مجموعه میشود:
$$n(A-B)+n(B-A)$$
ت) از هیچ یک از این دو شرکت خرید نکردهاند.
$$n(U)-n(A\bigcup B) \\ ۱۱۰-۹۵=۱۵$$


