گام به گام ریاضی دهم | درس 1: مجموعه های متناهی و نامتناهی

1 الف) مجموعه $\mathbb{R}-\mathbb{Q}$ چه نام دارد؟ آن را روی شکل مقابل هاشور بزنید و دو عضو دلخواه از آن را در ناحیهٔ هاشور خورده بنویسید.

مجموعه اعداد گنگ نام دارد و با $Q'$ نمایش داده می‌شود.

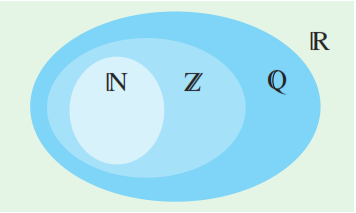
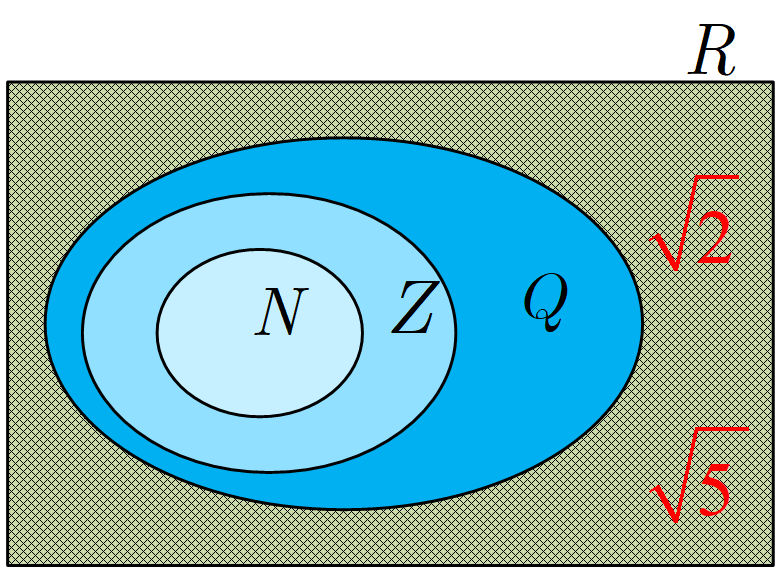
ب) دو عددگویا مثال بزنید که عدد صحیح نباشند و آنها را روی شکل مقابل در محل مناسب بنویسید.

$-\frac{3}{4},\frac{2}{7}$

پ) اعداد زیر را روی شکل و در محل مناسب بنویسید.
$\sqrt{17},0,200,\frac{\pi }{2},2/6,2\sqrt{5},-\frac{25}{3},-9$

ت) مجموعه اعداد صحیح غیر حسابی را با نمایش اعضا بنویسید.

$Z-W=\left\{ -1,-2,-3,-4,... \right\}$

ث) مجموعهٔ $W-\mathbb{N}$ چند عضو دارد؟

فقط یک عضو دارد و آن عدد صفر است.$W-N=\{0\}$

2- هریک از اعداد داده شده را در یکی از جاهای مشخص شده روی محور بنویسید. کدام یک از این شش عدد گنگ‌اند؟ زیر آنها خط بکشید.
$2/45,\frac{-7}{2},6,-4/9,\pi ,-\sqrt{2}$

اعداد $-\sqrt{2}$ و $\pi$ اعدادی گنگ هستند

اگر $a$ و $b$ دو عدد حقیقی دلخواه باشند، به طوری که $a \lt b$ آنگاه جدول زیر را کامل کنید.

نمایش هندسه‌ای	نمایش مجموعه‌ای	بازه	نوع بازه
	$\{x\in \mathbb{R}|a \lt x \lt b\}$	(a,b)	باز
	$\{x\in R|a \le x \le b\}$	[a,b]	بسته
	$\{x\in R|a \le x \lt b\}$	[a,b)	نیم باز
	$\{x\in R|a \lt x \le b\}$	(a,b]	نیم باز
	$\{x\in \mathbb{R}|1 \lt x \le 5\}$	(1,5]	نیم باز
	$\{x\in R|-3 \lt x \le 2\}$	[-3,2)	نیم باز

اگر $a$ عدد حقیقی دلخواهی باشد، جدول زیر را کامل کنید.

نمایش هندسه‌ای	نمایش مجموعه‌ای	بازه	نوع بازه
	$\{x\in \mathbb{R}|x>a\}$	$(a,+\infty )$	باز
	$\{x\in \mathbb{R}|x\ge a\}$	$[a,+\infty )$	نیم باز
	$\{x\in \mathbb{R}|x\le a\}$	$(-\infty ,+\infty )$	نیم باز
	$\{x\in \mathbb{R}|x \lt a\}$	$(-\infty ,a)$	باز
	$R$	$(-\infty ,+\infty )$	باز
	$\{x\in \mathbb{R}|x\le 3\}$	$[3,+\infty )$	نیم باز
	$\{x\in \mathbb{R}|x<5\}$	$(-\infty ,5)$	باز

1- درستی یا نادرستی عبارت‌های زیر را مشخص کنید:

الف) $\frac{4}{3}\in [\frac{1}{2},2)$ ← درست

ب) $-2\in (-2,0]$ ← نادرست

پ) $0\in (-2,0]$ ← درست

ت) $-2\in (-2,0]$ ← درست

ث) $-1\in \{-2,0\}$ ← نادرست

ج) $[-1,2]\subseteq (-1,2)$ ← نادرست

چ) $\{0,1\}\subseteq [-1,2)$ ← نادرست

ح) $\varnothing \subseteq (-17,0]$ ← درست

خ) $[2,5)=(2,5]$ ← نادرست

د) $\sqrt{2}\in (0,1)$ ← نادرست

2- هر یک از اعداد زیر عضو یک یا چند تا از بازه‌های داده شده هستند. هر عدد را به بازه یا بازه‌های نظیر آن وصل کنید.

$0/2$ ← $(-2,3)$ و $(\frac{-1}{2},\frac{1}{2}]$

$6/022\times {{10}^{23}}$ ← $[3,+\infty )$

$\frac{-5}{2}$ ← به هیچکدام از بازه ها تعلق ندارد.

$-500$ ← $(-\infty ,-4)$

$\sqrt{3}$ ← $[1,4]$ , $(-2,3)$

$-2$ ← $[-2,0)$

3- نمایش هندسی دو بازه $A=(-4,2] و B=(-1,3]$ را روی محور زیر رسم کنید و سپس حاصل عبارت‌های زیر را بنویسید.

الف) $A\bigcap B$

$A\bigcap B=(-1,2]$

ب) $A\bigcup B$

$A\bigcup B=(-4,3]$

پ) $A-B$

$A-B=(-4,-1]$

ت) $B-A$

$B-A=(2,3]$

فرض کنید A مجموعهٔ اعداد طبیعی کمتر از 4 و B مجموعهٔ اعداد صحیح کمتر از 4 باشد.

الف) این دو مجموعه را با نمایش اعضای آنها مشخص کنید.

$A=\{1,2,3\}$
$B=\{3,2,1,0,-1,...\}$

ب) A چند عضو دارد؟ 3 عضو

پ) دربارهٔ تعداد اعضای B چه می‌توان گفت؟

تعداد اعضای مجموعه B بی‌شمار است.

1- متناهی یا نامتناهی بودن هر یک از مجموعه‌های زیر را مشخص کنید. دربارهٔ مجموعه‌های متناهی سعی کنید تعداد دقیق یا تقریبی اعضای هر یک از آنها را بنویسید.

2- دو مجموعهٔ متناهی نام ببرید.

الف) مجموعه اعداد زوج کمتر از 100
ب) مجموعه حالت‌هایی که در پرتاب دو تاس اتفاق می‌افتند.

3- دو مجموعهٔ نامتناهی مثال بزنید که یکی از آنها زیر مجموعهٔ دیگری باشد.

مجموعه اعداد گویا $(Q)$ و مجموعه‌ی اعداد صحیح $(Z)$ که $Z\subseteq Q$

4- دو مجموعهٔ نامتناهی مثل A و B مثال بزنید که $A\subseteq B$ بوده و $B-A$ تک عضوی باشد.

A را مجموعه اعداد طبیعی (N) و B را مجموعه اعداد حسابی (W) در نظر بگیرید در این صورت داریم؛
$A\subseteq B$
$B-A=\{0\}$

تذکر: تعداد اعضای برخی از مجموعه‌های متناهی ممکن است بسیار زیاد باشد؛ با این حال با داشتن امکانات لازم و صرف وقت کافی ممکن است بتوان تعداد آنها را به دست آورد.

الف) $\frac{1}{3}$ عددی بین 0 و 1 است.چهار عدد گویای دیگر از بازهٔ (0،1) بنویسید و جواب خود را با جواب‌های دوستانتان مقایسه کنید.

$\frac{300}{401},\frac{17}{18},\frac{5}{2016},\frac{1}{8}$
تنوع عددها بسیار زیاد است.

ب) آیا می‌توان بین 0 و 1 به هر تعداد دلخواه عدد گویا ارائه کرد؟ 

پ) در مورد متناهی یا نامتناهی بودن اعداد گویای موجود در بازهٔ (0، 1) چه نتیجه‌ای می‌گیرید؟

بین صفر و یک، تعداد نامتناهی عدد گویا وجود دارد.

ت) در مورد متناهی یا نامتناهی بودن $\mathbb{Q}$ می‌توان گفت؟

$Q$ مجموعه‌ای نامتناهی است.

ث) اگر A دارای یک زیر مجموعهٔ نامتناهی باشد، آنگاه A یک مجموعه نامتناهی خواهد بود.

1- فرض کنید $U$ مجموعهٔ تمام مضرب‌های طبیعی عدد 5 باشد.

الف) $U$ را با نمایش اعضای آن بنویسید.

$A=\{5,10,15,20,...\}$

ب) $U$ متناهی است یا نامتناهی؟ نامتناهی

پ) یک زیرمجموعهٔ متناهی از $U$ بنویسید.

$B=\{10,20,...,80,90\}$

ت) دو زیر مجموعهٔ نامتناهی مانند $C$ و $D$ از $U$ بنویسید؛ به طوری که $C\subseteq D$.

$D=\{10,20,30,40,...\}$
$C=\{100,200,300,...\}$

2- متناهی یا نامتناهی بودن مجموعه‌های زیر را مشخص کنید.

الف) مجموعه اعداد طبیعی. نامتناهی

ب) مجموعه شمارنده های طبیعی عدد 3.

متناهی است زیرا؛
$\{1,2,3,4,6,9,12,18,36\}$

پ) بازه$(\frac{1}{4},\frac{1}{2})$. نامتناهی

ت) $A=\{x\in \mathbb{N}|1 \lt x \lt 2\}$

متناهی $A=\{\}$

ث) مجموعهٔ مضرب‌های طبیعی عدد 100. نامتناهی

3- دو مجموعهٔ نامتناهی مثال بزنید که اشتراک آنها مجموعه‌ای متناهی باشد.

مجموعه اعداد طبیعی $(N)$ و مجموعه‌ی اعداد صحیح بین 5- تا 5+ $(A)$.
$\left. \begin{matrix} \text{ }\!\!~\!\!\text{ }\!\!~\!\!\text{ }N=\{1,2,3\}\begin{matrix} {} & {} & {} \\ \end{matrix}\text{ }\!\!~\!\!\text{ } \\ \text{ }\!\!~\!\!\text{ }\!\!~\!\!\text{ }A=\{-4,-3,...,3,4\}\text{ }\!\!~\!\!\text{ } \\ {} \\ \end{matrix} \right\}\Rightarrow A\bigcap{N}=\{1,2,3,4\}$

4- حاصل هر یک از مجموعه‌های زیر را با رسم بازه‌های آنها روی یک محور به دست آورید:

الف) $(-3,0)\bigcup (-2,5]$

$(-3,0)\bigcup (-2,5]=(-3,5]$

ب) $(-\infty ,6]\bigcap (2,9)$

$(-\infty ,6]\bigcap{(2,9)}=(2,6]$

پ) $(3,+\infty )\bigcap (6,10]$

$(3,+\infty )\bigcap (6,10]=(6,10]$

ت) $(-\infty ,1)\bigcup (1,+\infty ]$

$(-\infty ,1)\bigcup (1,+\infty ]=R$

ث) $(3,+\infty )-[2,4)$

$(3,+\infty )-[2,4)=[4,+\infty )$

ج) $(2,4)-[3,+\infty )$

$(2,4)-[3,+\infty )=[2,3]$

5- مجموعهٔ $\mathbb{R}-\{3\}$ را روی محور نشان دهید و سپس آن را به صورت اجتماع دو بازه بنویسید.

$R-\{3\}=(-\infty ,3)\bigcup (3,+\infty )$

6- اگر $A\subseteq B$ و $B$ مجموعه‌ای متناهی باشد، آنگاه $A$ متناهی خواهد بود یا نامتناهی؟

تعداد اعضای A از B کمتر است، بنابراین A هم متناهی خواهد بود.